Extracting Sensitive Information from Aggregated Data - Part 1

One common challenge is convincing people that aggregate information can still qualify as personal data under the GDPR. By “aggregate information,” I refer to statistical summaries such as sums, medians, and means derived from a confidential dataset, or even the parameters of a trained machine learning model.

In this post, I start with the simplest case: demonstrating how sensitive personal data can be reconstructed from the results of a series of SUM queries performed on a confidential dataset. I also demonstrate how machine learning can be used to extract sensitive data from any aggregate information. In a follow-up post, I’ll explore how an attacker can strategically minimize the number of queries needed to reconstruct every record in the dataset.

For the sake of illustration, consider the following hospital dataset.

#	Name	ZIP	Gender	Blood sugar
1	John Smith	32453	Male	4.3
2	Jeremy Doe	43813	Male	5.2
3	Susan Atkinson	43765	Female	6.1
4	Eve Brown	32187	Female	3.2
5	Joseph Sky	33745	Male	7.1
6	Alison Moon	22983	Female	6.2

Here, ZIP and Gender (in green) are considered public attributes, while Name and Blood Sugar (in red) are private. We show how statistical queries (such as sums or averages) over Blood Sugar can potentially expose an individual's blood sugar value - even when each query is computed across multiple records.

Following SQL syntax, a query consists of a WHERE clause, which filters records from the dataset based on public attributes, and an aggregate function that summarizes a private attribute over the selected records. For example, the query SELECT SUM("Blood sugar") WHERE Gender = "Male" uses the predicate Gender = "Male" and the aggregate function SUM, returning the result 16.6 (the sum of blood sugar values for males: $4.3 + 5.2 + 7.1$ ).

It is not hard to see that answering the following queries reveal the blood sugar level of the second record (Jeremy Doe), even though each query covers at least two records.

Query 1: SELECT SUM("Blood sugar") FROM Dataset; Result: 32.1
Query 2: SELECT SUM("Blood sugar") FROM Dataset WHERE Gender = "Female"; Result: 15.5
Query 3: SELECT SUM("Blood sugar") FROM Dataset WHERE ZIP > 32000 and ZIP < 35000 AND Gender = "Male"; Result: 11.4

To see why, notice that Query 1 and 2 reveal the total blood sugar level of all males (subtract the result of Query 2 from that of Query 1), and Query 3 selects only Record 1 and 5. Therefore, taking the difference of the result of Query 3 and the total blood sugar of all males, we obtain the exact blood sugar level of Record 2.

To make it more formal, let $x_{i}$ denote the unknown (private) Blood sugar value of record $i$ . Each query along with its result can be represented by a linear equation as follows:

Query 1: $x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} = 32.1$
Query 2: $x_{3} + x_{4} + x_{6} = 15.5$
Query 3: $x_{1} + x_{5} = 11.4$

Or, with matrix notation:

A x = b

where

A = [\begin{matrix} 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 & 0 \end{matrix}]

x = (x_{1}, x_{2}, \dots, x_{6})^{T}

b = (32.1, 15.5, 11.4)^{T}

The task is to check if any $x_{i}$ can be unambiguously determined, or, in the worst case, whether the entire system of equations has a unique solution (i.e., all $x_{i}$ can be uniquely identified). If that is the case, the queries specified by matrix $A$ cannot be answered without revealing individual private attribute values.

Why?

Seemingly, solving this linear system for any unknown, without associating it with a specific individual (e.g., Jeremy Doe), should not imply a privacy breach under GDPR. According to GDPR, information is considered personal only if it can be linked to an identified or identifiable person. If the attacker only has access to public attributes (marked in blue), they likely cannot link the value of $x_{2}$ to Jeremy Doe. However, the attacker may have additional background knowledge that could help identify Jeremy, even without access to the “Name” attribute. For example, they could know from another source (such as social platforms, voters registration data, browsing data, AI chat bots) that Jeremy visited a hospital and that his ZIP code starts with 438**. If this additional information is easily accessible, it could allow the attacker to determine Jeremy’s blood sugar value using the reconstruction attack described in this post. As a result, the outcomes of Queries 1, 2, and 3 may qualify as personal or sensitive data under GDPR when the attacker has "reasonable" access to the necessary background knowledge.

Which records can be reconstructed?

Given a linear system of equations $A x = b$ , where $b = {b_{1}, \dots, b_{m}}$ , $A \in R^{m, n}$ , and row $i$ of $A$ corresponds to query $q_{i}$ . In general, an unknown $x_{i}$ can be unambiguously determined if the following conditions are met:

The system must be consistent, meaning that the vector $b$ is a linear combination of the columns of $A$ . In other words, $b$ must lie within the column space of $A$ . This is verified by checking if $rank (A) = rank ([A | b])$ , where $[A | b]$ is the augmented matrix formed by appending $b$ as a column to $A$ .
The $i$ th column of $A$ must be linearly independent of the remaining columns. To check this, remove the $i$ th column from $A$ and compute the rank of the resulting matrix. If the rank decreases, it confirms that the $i$ th column is linearly independent.

In the above example, each query was answered faithfully, hence the linear system is consistent. To illustrate the second condition, let's reformulate $A x = b$ as:

x_{1} \cdot [\begin{matrix} 1 \\ 0 \\ 1 \end{matrix}] + x_{2} \cdot [\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}] + x_{3} \cdot [\begin{matrix} 1 \\ 1 \\ 0 \end{matrix}] + x_{4} \cdot [\begin{matrix} 1 \\ 1 \\ 0 \end{matrix}] + x_{5} \cdot [\begin{matrix} 1 \\ 0 \\ 1 \end{matrix}] + x_{6} \cdot [\begin{matrix} 1 \\ 1 \\ 0 \end{matrix}] = [\begin{matrix} 32.1 \\ 15.5 \\ 11.4 \end{matrix}]

This expression shows that vector $b$ is a linear combination of the columns of the matrix $A$ , weighted by the unknowns $x_{1}, \dots, x_{6}$ . Here, the contribution of the second column $(1, 0, 0)^{T}$ to the linear combination $b$ is unique and cannot be replicated by any other column or combination of columns from the matrix $A$ . Indeed, adding this column to matrix

[\begin{matrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 \end{matrix}]

increases its rank by one:

import numpy as np
from numpy.linalg import matrix_rank

# Define the matrix A and vector b
A = np.array([
[1, 1, 1, 1, 1, 1],
[0, 0, 1, 1, 0, 1],
[1, 0, 0, 0, 1, 0]
])

b = np.array([32.1, 15.5, 11.4])

for col in range(A.shape[1]):
	print (f"Unknown x_{col+1} can be uniquely determined:",
	matrix_rank(A) != matrix_rank(np.delete(A, col, axis=1)))

which produces:

Unknown x_1 can be uniquely determined: False
Unknown x_2 can be uniquely determined: True
Unknown x_3 can be uniquely determined: False
Unknown x_4 can be uniquely determined: False
Unknown x_5 can be uniquely determined: False
Unknown x_6 can be uniquely determined: False

However, this uniqueness does not apply to the other columns which appear multiple times in the matrix. After multiplying out these (linearly dependent) columns we have:

(x_{1} + x_{5}) \cdot [\begin{matrix} 1 \\ 0 \\ 1 \end{matrix}] + x_{2} \cdot [\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}] + (x_{3} + x_{4} + x_{6}) \cdot [\begin{matrix} 1 \\ 1 \\ 0 \end{matrix}] = [\begin{matrix} 32.1 \\ 15.5 \\ 11.4 \end{matrix}]

Since all the three column vectors are linearly indepedent in this reformulated version, we can uniquely determine their weights: $x_{2}$ , the sum of $x_{1}$ and $x_{5}$ , and the sum of $x_{3}$ , $x_{4}$ , and $x_{6}$ . However, we cannot tell how these sums are shared among their respective variables. This implies that the original linear system as a whole still has an infinite number of solutions.

In general, if $rank ([A | b]) = rank (A) < n$ , as in the example above, the system is underdetermined because there are fewer linearly independent queries (rows) than unknowns. As a result, the solution space typically has infinitely many solutions. Imposing constraints, such as requiring $x$ to be an integer or enforcing sparsity (at most $rank (A)$ non-zero entries in $x$ ) can reduce the solution space to a finite set.

If $rank ([A | b]) = rank (A) = n$ , meaning $A$ is square and full rank, the system has a unique solution given by $x = A^{- 1} b$ . In that case, all columns are linearly independent and therefore every unknown $x_{i}$ can be unambiguously determined. It may happen that we have more rows than columns because some rows/queries are linearly dependent, but the number of linearly independent queries is at most $n$ .

Solving the equations

There are a couple of techniques to solve (or approximate) a linear system; any matrix decomposition technique (e.g., QR or LU decomposition) can be applied on the augmented matrix $A^{*}$ . Here, we rather use a more versatile optimization technique which provides an approximation of $x$ irrespective of the rank of $[A | b]$ :

x^{'} = \arg min_{x \in R^{n}} | | A x - b | |_{2}

where $| | \cdot | |_{2}$ denotes the Euclidean distance ( $L_{2}$ -norm).

The solution of this optimization problem has a closed form $x^{'} = \hat{A} b$ , where $\hat{A}$ is the pseudo-inverse (or Moore-Penrose inverse) of $A$ . If $A$ is invertible, then $A^{- 1} = \hat{A}$ . This optimization technique is widely known as Ordinary Least Squares (OLS) or linear regression in machine learning terminology. OLS and pseudo-inverse computations are supported by many linear algebra libraries and machine learning frameworks, including scikit-learn, torch, numpy.

For example, in numpy:

# Solve the system using NumPy's least-squares method (since A is not square)
x_prime = np.linalg.lstsq(A, b, rcond=None)[0]

print ("Solution:", x_prime)

and the output:

Solution: [5.7 5.2 5.16666667 5.16666667 5.7 5.16666667]

where Jeremy Doe's blood sugar level ( $x_{2}$ ) is accurately computed. Notice that the sums $x_{1} + x_{5} = 11.4$ and $x_{3} + x_{4} + x_{6} = 15.5$ are correct. OLS finds the solution with the smallest $L_{2}$ -norm, which occurs when the sums are evenly distributed among their respective variables.

Incorporating background knowledge as constraints

The above solution can be made more accurate if we incorporate prior knowledge about the unknowns as additional constraints into the optimization problem. As long as these constraints are convex, efficient convex solvers can be used to obtain a better approximation of $x$ . For example, knowing that John Smith’s blood sugar level is less than 5 could improve the accuracy of the approximation for Joseph Sky’s blood sugar level:

import cvxpy as cvx

x = cvx.Variable(A.shape[1])
objective = cvx.Minimize(cvx.sum_squares(A @ x - b))
# First record is smaller than 5
constraints = [x[0] <= 5]
  
prob = cvx.Problem(objective, constraints)
prob.solve()

print ("Solution:", x.value)

and the output is:

Solution: [1.15961346e-04 5.20000027e+00 5.16666694e+00 5.16666694e+00 1.13998846e+01 5.16666694e+00]

This is quite dummy as no one has a blood sugar level of less than 0.01. Let's add another constraint that all values must be larger than 3:

objective = cvx.Minimize(cvx.sum_squares(A @ x - b))
# Constraint 1: First record is less than 5
# Constraint 2: All records are larger than 3
constraints = [x[0] <= 5, x >= 3]
  
prob = cvx.Problem(objective, constraints)
prob.solve()

print ("Solution:", x.value)

The output is:

Solution: [4.06728662 5.20000018 5.1666669 5.1666669 7.3327138 5.1666669 ]

This looks much more realistic! This approximation is closer to the true solution $x$ and suggests that Joseph Sky may have hyperglycemia.

The private attribute $x$ may sometimes be binary in practice, such as indicating whether a patient has AIDS or not. More generally, a counting query using the aggregate function COUNT returns the number of records that satisfy a given predicate. Introducing such an integer constraint turns the problem into an instance of Integer Linear Programming (ILP) which is NP-complete in general. While cvxpy supports mixed integer linear programming (MILP) solvers, a more practical and efficient approach is to round each element of $x^{'}$ (the OLS solution) to the nearest integer, obtaining a final approximation of the original vector $x$ .

Handling many queries and records

Even convex optimization, including OLS, can become quite slow and memory-intensive for large datasets with many queries as they operate on the entire matrix $A$ . Iterative methods, on the other hand, generate a sequence of approximate solutions that converge progressively closer to the exact solution with each iteration. These methods are typically less computationally demanding, though their convergence rate depends on the properties of matrix $A$ . Common iterative methods include the Jacobi method, the Conjugate Gradient method, or the L-BFGS. However, these algorithms may still be inefficient when dealing with a large number of equations (queries) and not only unknowns (records).

To address this, we present a solution based on stochastic gradient descent (SGD), which uses only one row of the matrix $A$ per iteration. This approach is particularly appealing in online scenarios where queries must be audited in real-time, or where storing the entire query set is impractical due to legal constraints or the sheer number of queries.

We aim to minimize the function $R (x) = | | b - A x | |_{2}^{2} = \sum_{j = 1}^{m} r_{j} (x)$ , where $r_{j} (x) = (b_{j} - A_{j} x)^{2}$ is the residual error of the $j$ th equation (query), with $A_{j}$ being the $j$ th row of matrix. Gradient descent is an iterative method that improves the solution step by step. In each iteration, it calculates the gradient $\nabla_{x} R (x)$ and updates the current estimate $x^{(i)}$ by moving in the opposite direction of the gradient:

\begin{aligned} x^{(i + 1)} & = x^{(i)} - η \cdot \nabla_{x} R (x) \\ = x^{(i)} - η \cdot \nabla_{x} \sum_{j = 1}^{m} r_{j} (x) \end{aligned}

Since $r_{j}$ is convex, their sum $R (x)$ is also convex, which means that, if we set the step size $η$ well (just not too big and not too small), the above procedure will progressively get closer to the global minimum of $R (x)$ .

However, in each descent step, we still iterate over all queries, making this approach computationally expensive and not better than other iterative techniques. To improve efficiency, stochastic gradient descent exploits that minimizing $R (x)$ is equivalent to minimizing its mean $R (x) / m$ , which is the expected value of $R (x)$ if queries are chosen uniformly at random:

\begin{aligned} x^{(i + 1)} & = x^{(i)} - η \cdot \nabla_{x} R (x) / m \\ = x^{(i)} - η \cdot \frac{1}{m} \sum_{j = 1}^{m} \nabla_{x} r_{j} (x) \\ = x^{(i)} - η \cdot E_{j \sim U (1, m)} [\nabla_{x} r_{j} (x)] \end{aligned}

where $U (1, m)$ represents the uniform distribution over integers in $[1, m]$ . Instead of summing over all $m$ queries, we approximate the expected value by randomly sampling one query at each iteration: in each iteration $i$ , a single query (or equation) $j$ is randomly selected, and the gradient’s expected value across all queries is estimated with the gradient of just this one query:

x^{(i + 1)} \approx x^{(i)} - η \cdot \nabla_{x} r_{j} (x)

The gradient is given by:

\nabla_{x} r_{j} (x) = - 2 (b_{j} - A_{j} x^{(i)}) A_{j}^{T}

If we set the step size $η = \frac{1}{2 | | A_{j} | |_{2}^{2}}$ , this iterative approach becomes the randomized version of Kaczmarz's method :

x^{(i + 1)} = x^{(i)} + \frac{(b_{j} - A_{j} x^{(i)}) A_{j}^{T}}{| | A_{j} | |_{2}^{2}}

Kaczmarz’s method has an intuitive geometric interpretation: starting from an initial candidate solution $x^{(0)}$ , an improved solution $x^{(i + 1)}$ is found by projecting $x^{(i)}$ onto the hyperplane defined by the randomly chosen $j$ -th equation, $⟨ A_{j}, x ⟩ = b_{j}$ .

Why?

Let $x_{p}$ be the projection of $x^{(i)}$ onto hyperplane $A_{j} x = b_{j}$ and $x^{'}$ be any reference point that lies on this hyperplane. Since vector $A_{j}$ is orthogonal to this hyperplane, $x_{p}$ can be described as the result of shifting $x^{(i)}$ by the projection of vector $(x^{(i)} - x^{'})$ to vector $A_{j}$ . The vector $(x^{(i)} - x^{'})$ represents the displacement from a reference point $x^{'}$ to the point $x^{(i)}$ .

How does it look like in two dimensions?

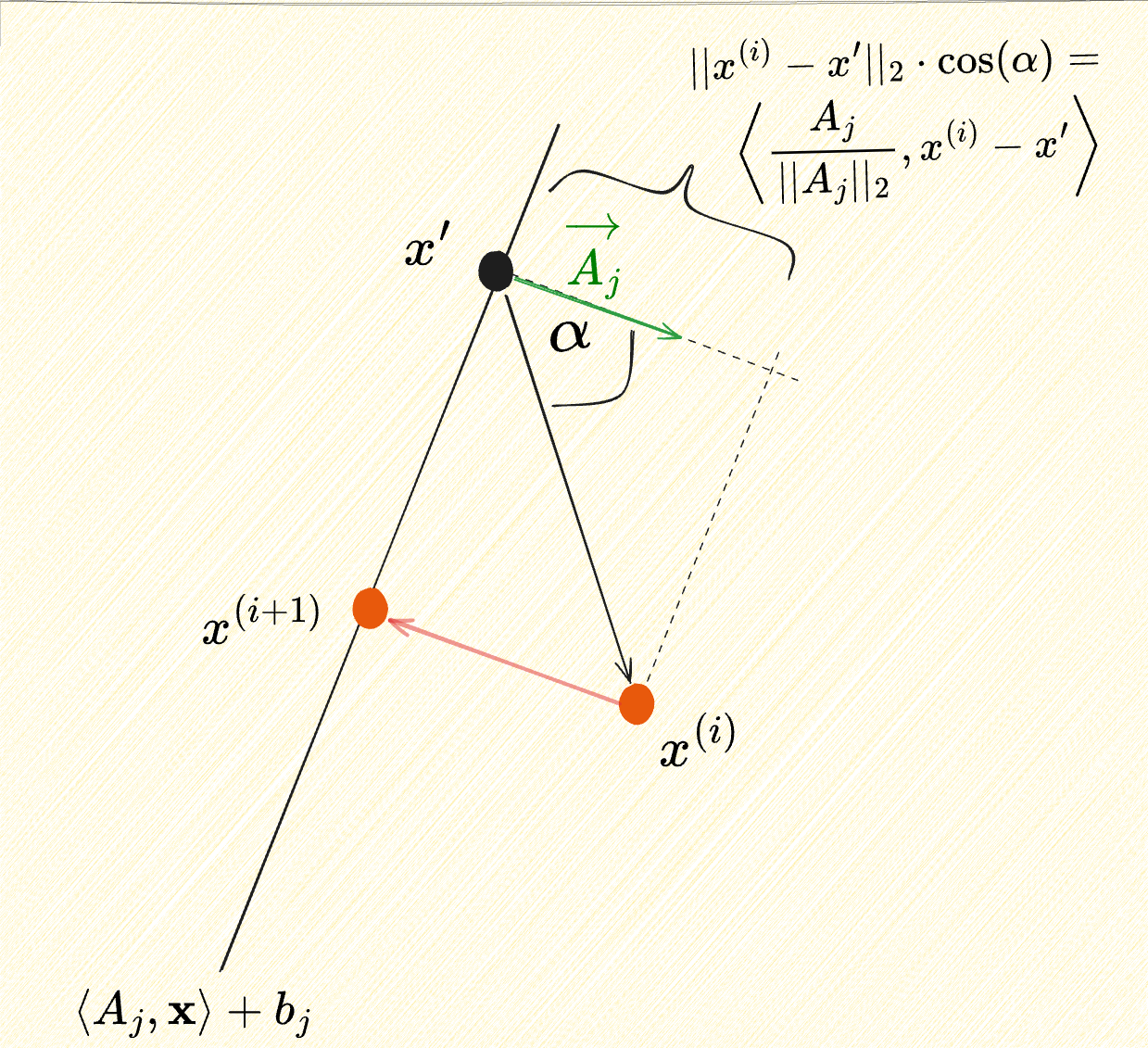
Projection.excalidraw.png

The projectionof this displacement vector onto $A_{j}$ is given by

⟨ \frac{A_{j}}{| | A_{j} | |_{2}}, x^{(i)} - x^{'} ⟩ \frac{A_{j}^{T}}{| | A_{j} | |_{2}}

and hence

\begin{aligned} x_{p} & = x^{(i)} - ⟨ \frac{A_{j}}{| | A_{j} | |_{2}}, x^{(i)} - x^{'} ⟩ \frac{A_{j}^{T}}{| | A_{j} | |_{2}} \\ = x^{(i)} - ⟨ A_{j}, x^{(i)} - x^{'} ⟩ \frac{A_{j}^{T}}{| | A_{j} | |_{2}^{2}} \\ = x^{(i)} - (⟨ A_{j}, x^{(i)} ⟩ - ⟨ A_{j}, x^{'} ⟩) \frac{A_{j}^{T}}{| | A_{j} | |_{2}^{2}} \\ = x^{(i)} + (b_{j} - ⟨ A_{j}, x^{(i)} ⟩) \frac{A_{j}^{T}}{| | A_{j} | |_{2}^{2}} \end{aligned}

for any $x^{'}$ such that $⟨ A_{j}, x^{'} ⟩ = b_{j}$ .

The steps of the process in 2D are shown in the figure below, where each equation is a line, and their single intersection point in the center is the unique solution to the whole system of equations. For consistent systems, $x^{(i)}$ gradually converges to this unique solution.

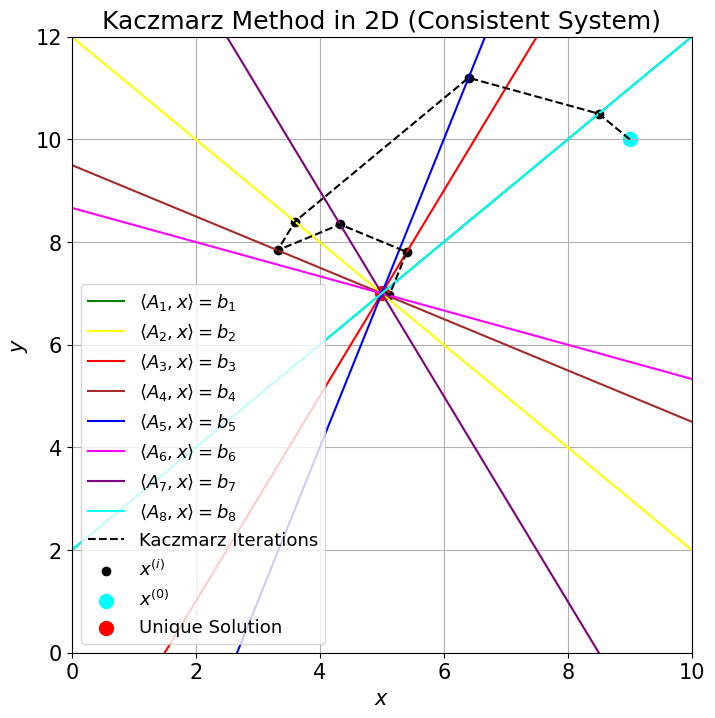
There are other variants of Kaczmarz's method that have been adapted even for inconsistent systems.

Adding constraints is also possible. For example, box constraints $ℓ \leq x \leq u$ can be incorporated by introducing a change of variables as follows:

\arg min_{x : ℓ \leq x \leq u} R (x) = \arg min_{z} R (ℓ + (u - ℓ) ⊙ sigmoid (z))

where $⊙$ denotes the element-wise product between vectors, and $sigmoid (z) = 1 / (1 + \exp (- z))$ is applied element-wise to map each entry of $z$ into the range $(0, 1)$ . This transformation ensures that the objective function remains differentiable, allowing gradient descent to be applied as in the unconstrained case. Other techniques, like barrier functions, can also handle constraints.

Continuing our hospital example, suppose the blood sugar levels have lower bounds $ℓ = (3, 3, 3, 3, 3, 3)$ and upper bounds $u = (5, 10, 10, 10, 10, 10)$ for our six records. Using PyTorch's automatic differentation framework, we can efficiently compute gradients and perform optimization under the given box constraints:

import torch

A_t = torch.tensor(A).float()
b_t = torch.tensor(b)
# compute gradient wrt x_t
x_t = torch.zeros(A.shape[1], requires_grad=True)

# Box constraints (l: min blood sugar, u: max blood sugar)
l = torch.tensor([3, 3, 3, 3, 3, 3])
u = torch.tensor([5, 10, 10, 10, 10, 10])
z = lambda x_t: l + (u - l) * torch.sigmoid(x_t)

learning_rate = 0.01

# Do 1000 SGD iterations
for i in range(1000):
	# select one row from A
	row = np.random.randint(0, A_t.shape[0])
	
	# objective function
	residual = torch.sum((A_t[row] @ z(x_t) - b[row])**2)
	# compute gradient
	residual.backward()
	
	with torch.no_grad():
		# gradient descent
		x_t -= learning_rate * x_t.grad
		x_t.grad.zero_()

print ("Solution:", z(x_t).detach().numpy())

that gives:

Solution: [4.0698786 5.2092214 5.165333 5.165333 7.3272643 5.165333 ]

This is close to the exact solution computed by cvxpy above!

Beyond linear queries

SUM, AVG, and COUNT are linear queries that can be audited using tools from linear algebra. However, auditing non-linear queries like MEDIAN, MAX, and MIN is more challenging. In fact, verifying exact disclosure for such queries may not even be feasible in polynomial time with respect to the dataset size $n$ or the number of queries $m$ .

One approach is to approximate the missing attribute values using heuristics like SAT solvers. Another is to apply stochastic gradient descent (SGD), as discussed above, if the queries are "approximately" differentiable functions of the attribute values. However, if the queries are non-convex functions of the records, then SGD does not guarantee convergence to the global optimum, meaning we cannot be sure that the solution it finds corresponds to the actual attribute values. Nevertheless, as in machine learning, we can hope that the solutions found are reasonably close to the actual solution.

Reconstruction is everywhere

Extraction "attacks" have long existed in computer science, though they were known by different names. For instance, error-correcting codes reconstruct corrupted data by solving a system of equations where the unknowns are the corrupted bits, bytes, or blocks of bytes. Linear error-correcting codes, like Reed-Solomon or BCH, operate in a finite field and are widely used in applications ranging from satellite communications to redundant data storage or QR codes where noise can corrupt information. A significant part of signal processing deals with the fast processing of naturally redundant data, such as images or voice. For example, compressive sensing can reconstruct high-quality MRI images from just a few linear measurements, greatly speeding up MRI acquisition.

Similarly, regular model training in machine learning (or AI) is a form of extraction attack. Here, the unknowns are the model parameters, and each training sample forms an equation. The queries represent the model, and optimization techniques like stochastic gradient descent are used to solve these equations like above. Extraction attacks can also target machine learning models. Whether the goal is to reconstruct the training data (with the unknowns being the sample features) or the model itself (with the unknowns being the model parameters), the process boils down to solving a system of (typically non-linear) equations. These attacks are especially relevant in light of recent regulations, such as the EU AI Act and GDPR.

So, it’s no surprise that as machine learning keeps improving, more advanced data extraction attacks will also appear. In the next post, I’ll show how an attacker can minimize the number of queries needed for data reconstruction by borrowing techniques from signal processing.